E dopo aver fatto un ripasso sui principali enti geometrici, aver parlato delle linee e dei punti, delle rettilinee e dei modi per dividere il piano con una sola linea, oggi proviamo a dividere il piano con due rettilinee…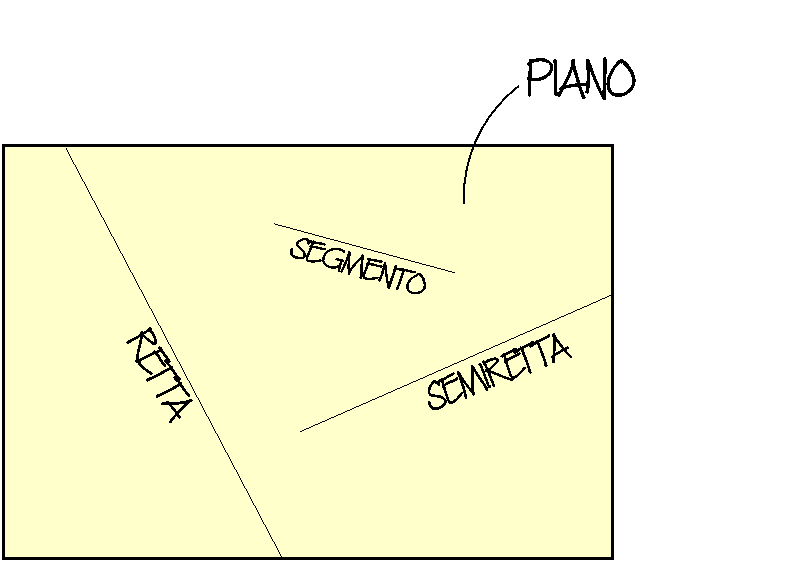
Cominciamo a provare con due segmenti….divideranno il piano?
Beh per qualcuno è stato immediato “…ma non possono…se non arrivano al confine del piano come si fa?”…altri invece hanno raccolto la provocazione e rilanciato “proviamo…magari si forma un dentro e un fuori!!!”
Vabbè, togliamoci i dubbi….proviamo! Sempre sul nostro piano a pavimento, con i nostri consueti strumenti…corde e bastoni…proviamo a suddividere il piano USANDO DUE SEGMENTI
Dopo prove, contestazioni, correzioni e incoraggiamenti siamo arrivati a questa conclusione….DUE SEGMENTI NON POSSONO MAI DIVIDERE IL PIANO IN DUE PARTI SEPARATE….anche se li mettiamo vicini vicini al confine del piano “…non vedi che un pelino è staccato…una formica passa!”
Passiamo ora alle semirette….con due semirette riusciamo a dividere il piano in due parti separate?
La discussione è stata accesa e ha visto i sostenitori del no in vantaggio per un certo tempo fino a che P. ha detto “….penso proprio di sì..le semirette arrivano al confine del piano…quindi…” e lì avanti….si è aperto un modo…e ancora quindi….proviamo per confermare o confutare le teorie!
Conclusione: DUE SEMIRETTE DIVIDONO IL PIANO SOLO SE SI INCONTRANO IN UN PUNTI, o meglio se hanno l’ORIGINE in comune…e formano due parti di piano che chiamiamo ANGOLI!
UN ANGOLO è CIASCUNA DELLE DUE PARTI O REGIONI DI PIANO DELIMITATE DA DUE SEMIRETTE CHE HANNO ORIGINE NELLO STESSO PUNTO!
Ogni coppia di semirette quindi forma DUE angoli “…che abbiamo capito maestra…non sono solo la puntina, come pensavamo noi…perchè anche nel calcio se facciamo il calcio d’angolo andiamo nella puntina!” “…non è solo la puntina, è tutto lo spazio fino alle semirette!”
Scriviamolo sui nostri quaderni!
Scriviamo anche come si chiamano le varie parti dell’angolo…non bisogna dimenticarsele…

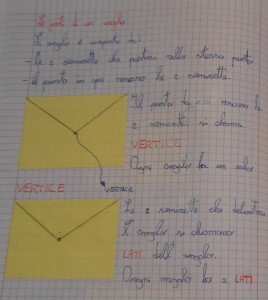
Ma se si formano DUE angoli alla volta come possiamo fare a far capire quale angolo consideriamo?
– facciamo un segno con il dito
– facciamo un puntino
– lo segniamo con un simbolo,
– gli diamo un nome
– mettiamo i punti con le lettere e poi lo nominiamo….
Le idee sono tantissime…proviamone alcune…
1- Coloriamo la parte di angolo che ci interessa “…maestra questo però sul pavimento non possiamo farlo altrimenti la bidella….!”
2- Usiamo dei simboli per segnare l’angolo considerato…ad esempio tracciamo tante rettilinee che partono dall’origine e che “riempiono” l’angolo che ci interessa….
3- Segniamo la parte di angolo che ci interessa, tracciando il suo confine…le semirette ci sono già per cui continuiamo a segnare da semiretta a semiretta…
“….che lungo però…ci vuole una super-corda!”
In realtà c’è un modo più veloce…si segna solo un archetto con una freccia che sta ad indicare il percorso da una semiretta all’altra e identifica l’angolo…l’archetto può essere ampio o anche piccino, ben vicino al vertice...
Anche questo lo riportiamo sul quaderno…
Ora che conosciamo gli angoli, facciamo alcuni esercizi pratici di costruzione sul pavimento….
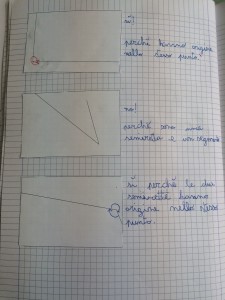
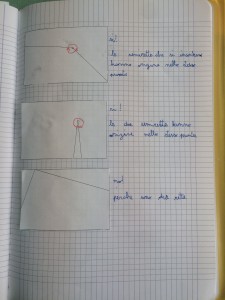
E ora osserviamo la scheda…cosa vediamo?
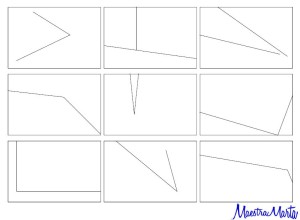
“…sono tutti angoli maestra!”
“…angoli???? ma se non ce ne sono di angoli…non vedi?”
“…ma alcuni sono angoli però!…o no???”
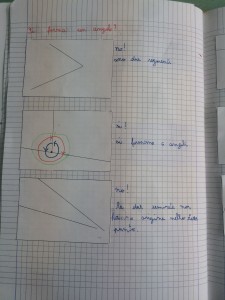
Analizziamoli e riportiamoli anche sul pavimento…in grande vediamo meglio…accanto ad ogni immagine sul quaderno scriveremo poi se si formano angoli, quanti e perchè sì o perchè no…e impariamo anche a segnare gli angoli con i colori e gli archetti che abbiamo visto prima…anche sul pavimento…con i gessi!


































Buongiorno. Grazie per la condivisione del tuo lavoro sugli angoli, che ho proposto efficacemente nelle mie classi. Pubblicherai anche qualcosa sui diversi tipi di angoli?
Ciao Marina, per ora sto lavorando sui poligoni e il perimetro.
In quarta farò il lavoro approfondito sugli angoli, la rotazione e i tipo di angoli per arrivare alla misurazione. Questo lavoro l’ho già fatto 5 anni fa ed è molto interessante, vi terrò aggiornati!
Grazie mille