Anche in 1a abbiamo da qualche tempo la nostra routine.
Dopo aver letto il libretto di Uri e imparato a scrivere i numeri oltre che in simboli sumeri anche scomponendo in modi diversi, compiliamo la scheda del “Numero del giorno” e poi ci confrontiamo.
Quanti modi diversi abbiamo trovato e messo in piramidi e bolle? Tra quali decine si trova il numero del giorno? Come lo scriverebbe Uri? E con le ten frame?
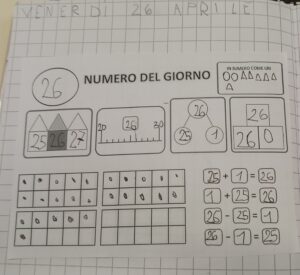
“Maestra ma i numeri del giorno sono più grandi del nostro pallottoliere! Dobbiamo aggiungere palline almeno 10!”
“Di più… perché 31 è più di 3 file di palline!”
“Vero allora facciamo che ne aggiungiamo due di file”
“…ma anche tre…non si sa mai!”
Ecco il file della scheda del Numero dei giorni:















